Artificial Life is the creation of living organisms and creatures by computer, as opposed to Real Life, which is made by nature.
Real life can be seen as a historical accident - inevitable given the right conditions, but only one instance of all the possible forms that could have been taken both at a physical level, and at the molecular substrate level - in our case carbon based.

The study of Artificial Life involves a large number of disciplines

Psychology : Philosophy : Anthropology : Computer Science : Hardware Design : Software Design : Virtual Reality : Evolutionary Theory : Genetics : Biochemistry

Why study Artificial Life?

- Carbon based life is only one instance.
- The computational aspect of A-life helps us understand real biology.
- The biological aspect of real life helps us solve computational problems.
- Emergent behavior could be a better model for complex systems and cognition

Emergent Behavior: Examples
- Flocking ( Boids by Reynolds )
- Swarm intelligence (ant, bee societies)
- Traffic Jams
- (Brooks/Maes): Subsumption architecture.
- Chaos Theory shows us that the result is more than the sum of its' parts.

Instead of just recreating nature, we are free through A-life to explore all the multitude of possible paths life could have taken but didn't. We don't have to do it in real-time and wait millions of years like in natural evolution, we can perform experiments in compressed time on the computer.
Artificial Life gives us a tool to understand the four levels of structure of living things on this planet: the ecosystem level, the organism level, the cellular level, and the molecular level. When the elements within these levels interact we get emergent behavior whose domain lies across these levels.

The Ecosystem Level

The best artificial model we have of this level is a population of individuals governed by a genetic algorithm .

The Organism Level

At this level we must model the behavior of the organism's sensory and nervous system within its environment. Experimentation at this level done at MIT by Brooks attempts to describe the creatures reactions from the bottom up, no explicit behavior is programmed into the insect-like robots they utilize, instead the use of neural-networks is used and the robot learns to walk in a couple of minutes.

The Cellular Level

This level is characterized by the self-replication ability of a single cell. One of the first researchers to recognize that we could simulate self-replication in an artificial system was John Von Neumann ; his cellular automata were able to simulate a universal Turing machine

The Molecular Level

Experimentation at this level involves using natural ribonucleic acid (RNA) in artificial ways, for example to solve mathematical sorting problems, and in acting as logic gates.

The Role of Chaos and Complexity Theory.

Complexity plays a role in A-Life because Life occurs at the thin border between chaotic and static systems.
We can see artificial examples of this in the "Game of Life" , where a single point change in the system can cause a ripple effect that will completely disturb; propagating the change throughout the system.
Random Boolean Networks provide an example of a stable system that is relatively immune to small local changes over the whole of the model

One of the simplest examples of the causes of complexity system is the Real number system, specifically Transcendental numbers (PI, e, roots), prime numbers, and the odd Integers.
We can see an example of odd odd-number behavior in action by looking at the "Hailstone Numbers".

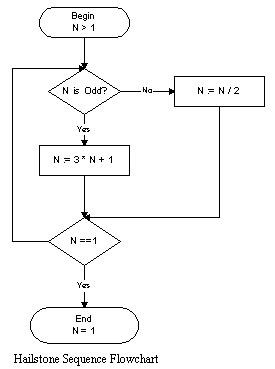
I first came across these number sequences in Scientific American in the mid 1980's, they are also called the 3n+1 numbers.
They exhibit the following behavior:

Now, you would expect to get predictable behavior, but the sequence is not intuitive, it goes up and down in an almost random fashion.
Another interesting thing, is that there is a small finite number of attractors (here maximum value) that can be reached from any integer.

For 27, there is a sequence of 111 numbers, with the maximum being 9232.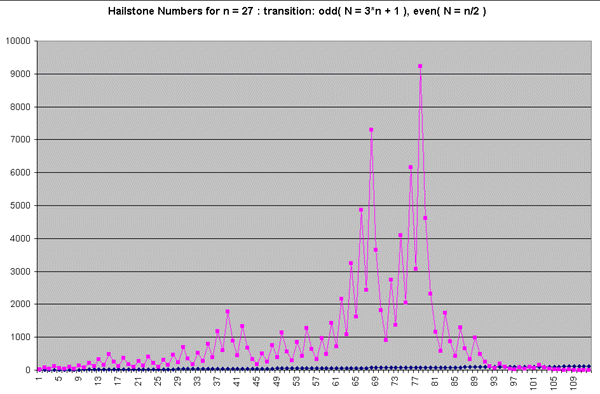

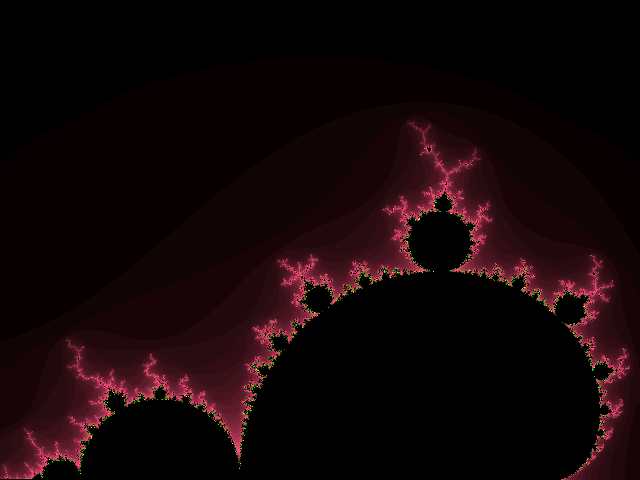
To summarize, we get complex behavior from 3 pieces of information (the number, and two algorithm steps), here the whole is more than the sum of it's parts.

Another more intricate example of chaotic behavior is a set that exists on the Complex number plane.
Benoit B. Mandelbrot, IBM Fellow, Discoverer of the Mandelbrot set, described the set he found - a kind of table of contents of Julia fractals for the equation Z(n) = Z(n-1)^2 + C (where C is the point on the complex 2-dimensional plane being examined).
When this equation is iterated, the time it takes for Z to spiral out past a radius of 2.0 becomes the color of the point.
The result of this is a fractal (fractional dimension) that has an infinite length around its circumference.